Base58 encoding is responsible for one of the most recognizable technical aspects of Bitcoin Core – the addresses!
This source file is responsible for a significant part of the algorithm that generates the addresses we use to send and receive Bitcoin.
If you’re not familiar with this encoding scheme, I recommend you read our article about base58 first to get an idea about why this encoding scheme does things the way it does.
So, let’s dive into the code!
base58.cpp
I’ve skipped the base58.h header because it’s basically just function declarations. We’ll go over each function here directly, so there’s no need to approach header and source separately.
Note that the code in base58 seems to have been based on base64 or some other C language encoding implementation. While the return values are standard C++, the inner workings are done using raw pointers and C style strings.
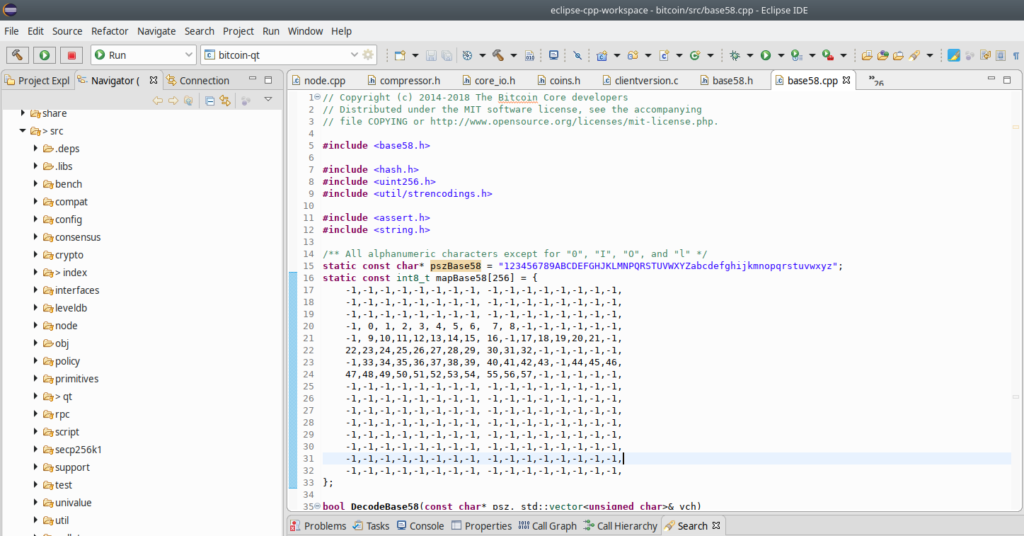
/** All alphanumeric characters except for "0", "I", "O", and "l" */
static const char* pszBase58 = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz";Fist, the base58 alphabet is defined. As the original source code comment explains, it’s all alphanumeric chars except for 0, I, O and L. This is done so Bitcoin addresses can be shared among users in printed form without ambiguities between the number 1 and letter l, zero and letter O and so forth. The alphabet is used in a very intuitive way: the values to be encoded represent indexes into the alphabet, so number zero will point to pszBase58where we find the digit 1. One will point to (pszBase58 + 1) and so on.
Next up we have the mapBase58 char array:
static const int8_t mapBase58[256] = {
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1, 0, 1, 2, 3, 4, 5, 6, 7, 8,-1,-1,-1,-1,-1,-1,
-1, 9,10,11,12,13,14,15, 16,-1,17,18,19,20,21,-1,
22,23,24,25,26,27,28,29, 30,31,32,-1,-1,-1,-1,-1,
-1,33,34,35,36,37,38,39, 40,41,42,43,-1,44,45,46,
47,48,49,50,51,52,53,54, 55,56,57,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
-1,-1,-1,-1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1,
};This looks like a matrix but it’s a single dimension array. The way this works is characters are looked up by their numerical value. If they land on a -1, then it’s an invalid character – not present in the encoding – so the subroutine will signal an error and return immediately. Otherwise the mapped value is read and used in the base58 algorithm we’ll discuss in a moment.
bool DecodeBase58(const char* psz, std::vector<unsigned char>& vch)
As the name implies, this decodes the string contained in psz and stores the result in the vch vector of unsigned char. So let’s take a look at how this is done.
First, it skips all leading spaces, skips and counts how many leading ones:
// Skip leading spaces.
while (*psz && IsSpace(*psz))
psz++;
// Skip and count leading '1's.
int zeroes = 0;
int length = 0;
while (*psz == '1') {
zeroes++;
psz++;
}Spaces are not valid base58 characters, so they’re assumed to have been inadvertently passed onto this function from unexpected user input. Blanks are tolerated at the beginning and end of the received string and is assumed to be noise and removed. Blanks within the string generate an immediate error and causes the decoding function to abort.
Zeroes are represented as one’s in base58, so each zero is counted and later added as a leading digit 1.
Now we allocate a std::vector of unsigned char to store our working string while it’s being decoded:
// Allocate enough space in big-endian base256 representation.
int size = strlen(psz) * 733 /1000 + 1; // log(58) / log(256), rounded up.
std::vector<unsigned char> b256(size);Here we estimate the length of a base256 vale based on base58. It uses the property that log_a(b) = log_x(b) / log_x(a). One is then added as a makeshift ceiling function.
Then the vector that’ll hold this new base256 string is declared, aptly named b256. A 256 byte translation table is used, so all encoded/decoded values are bounded to base 256.
It then asserts that the base58 map we’re using is indeed 256 characters long:
// Process the characters.
static_assert(sizeof(mapBase58)/sizeof(mapBase58[0]) == 256, "mapBase58.size() should be 256"); // guarantee not out of rangeIf you’re not familiar with this C language idiom, it’s an old trick used to measure array lengths. Unlike C++ STL containers or Java and other higher level languages, C does not store any meta information about its arrays like bounds, number of items currently contained in it, etc.
C language arrays are simply contiguous regions of memory, so there is no “length(array)” function in C.
The array length measuring trick in C goes like this: since the size of the array is statically known at compile time, the sizeof of the whole data structure (sizeof(mapBase58)) will be its total allocated length in bytes. The size of a single element can be taken from any element in the array, so sizeof(mapBase58[0]) is the size of the first character contained in the array, measured in bytes (= 1 byte). This assertion should never fail since mapBase58 is hard coded just a few lines above it. This code seems to have been glued together from other code where the translation table was originally externally provided.
Now we get to the main decoding loop:
while (*psz && !IsSpace(*psz)) {
// Decode base58 character
int carry = mapBase58[(uint8_t)*psz];
if (carry == -1) // Invalid b58 character
return false;
int i = 0;
for (std::vector<unsigned char>::reverse_iterator it = b256.rbegin(); (carry != 0 || i < length) && (it != b256.rend()); ++it, ++i) {
carry += 58 * (*it);
*it = carry % 256;
carry /= 256;
}
assert(carry == 0);
length = i;
psz++;
}While the current character (*psz) isn’t null and also isn’t a space (!IsSpace(*psz)), repeat loop.
First the numerical value of the current character (its ASCII code) is used as an index into mapBase58.If it lands on one of the -1 values then this is an invalid base58 character and the decoding function immediately returns.
A counter i is initialized to 0 and then we enter the inner for loop which turns the current value into a base 256 value. Let’s take a close look at this for loop’s declarations, conditionals and loop actions.
for (
std::vector<unsigned char>::reverse_iterator it = b256.rbegin();
(carry != 0 || i < length)
&&
(it != b256.rend());
++it,
++i
) {Its sole initialization is that of a reverse iterator into the b256 vector we declared earlier. This vector is initially empty and the reverse iterator runs from last to first element.
Fun fact: The processing is reversed because the b256 value is interpreted as a big endian number where the “rightmost” digit is the least significant (it’s how we read numbers, but Intel-based x86 computers work the other way around since they’re little endian).
There is then an injunction of two conditionals which must be simultaneously true for the loop to repeat. The second conditional is the simplest: “run as long as b256 hasn’t reached its beginning yet” (remember it’s a reverse iterator so the beginning is the rend(). ).
The first conditional is a bit more contrived. carrywhich we just read from the translation table must not be zero OR the string counter i must be less than the string length. The latter is pretty simple: run until the string is full processed. The first bit though requires us to dive into the for loop body:
carry += 58 * (*it);
*it = carry % 256;
carry /= 256;What’s happening here? First we get the base 10 value of a base 58 amount by multiplying by….58. If you’re not sure why this works, please review numerical bases (58 = 5 x 10^1 + 8 x 10^0). Then we take the current position in b256 (*it iterator dereference points into b256) and take the carry amount modulo 256. So we’ve just taken a base 58 amount, turned it into a decimal value and then took its 256 modulo. You may be thinking we’re losing data here? It would be lossy if we weren’t keeping track of the carry! That’s why in the next line we take the carry amount we’ve just modded by 256 and store the multiplier in it.
Original value = carry / 256 + carry MOD 256.
This is true for any number in any numerical base – just substitute 256 for any other base. (It’s the Euclidian algorithm from the year 300 BC!)
In short, the for loop is converting the base 58 characters into base 256 using a 2320 year old algorithm.
Now we have the iteration actions for the outer while loop.
assert(carry == 0);
length = i;
psz++;When the string ends, carry must be zero. Otherwise something went wrong in the base 256 conversion and we have a value carried-over from the last division. Euclid’s algorithm must add up to the original value perfectly with no carry after the last digit.
We set the length to i characters, add one to our original string pointer and iterate the while loop.
Now skip trailing spaces, if any. If the string isn’t at the end (null byte) then return false immediately as something’s wrong.
// Skip trailing spaces.
while (IsSpace(*psz))
psz++;
if (*psz != 0)
return false;Now we skip leading zeroes in base 256. Remember we counted the leading zeroes at the beginning of the decode function.
// Skip leading zeroes in b256.
std::vector<unsigned char>::iterator it = b256.begin() + (size - length);
while (it != b256.end() && *it == 0)
it++;Here we reserve space and add the zeroes back:
// Copy result into output vector.
vch.reserve(zeroes + (b256.end() - it));
vch.assign(zeroes, 0x00);Push decoded values back into return vector:
while (it != b256.end())
vch.push_back(*(it++));Language Note: If you’re new to C++ or if you learned modern C++ (from C++ 11 onwards) you might find it strange to return via a parameter, but this is very common in C and legacy C++ when return value copy elision wasn’t a thing yet. In early C++ if you returned a vector, it’d generate a copy. For big vectors this would be a major performance hog, so the results were often returned via an out-parameter. You can easily recognize out and in-out parameters in C++ because they’re not marked
const.
std::string EncodeBase58(const unsigned char* pbegin, const unsigned char* pend)
EncodeBase58 uses the same algorithm as Decode, except it works from base 256 to base 58. Notice how Euclid’s algorithm multiplies by the new base, 256, and not 58 as in the Decode function. Also the logarithm conversion formula mentioned earlier has its operands inverted because the conversion now goes the reverse way.
Everything else works the same as Decode.
Utility wrappers that use data from C++ containers to pass parameters to the Encode and Decode functions:
std::string EncodeBase58(const std::vector<unsigned char>& vch)
{
return EncodeBase58(vch.data(), vch.data() + vch.size());
}
bool DecodeBase58(const std::string& str, std::vector<unsigned char>& vchRet)
{
return DecodeBase58(str.c_str(), vchRet);
}C++ STL containers are aware of their length and other metadata. As mentioned earlier, this code is probably adapted from a C implementation where lower level arrays carry no meta-data. These two utility functions simply use C++ metadata to pass on down to the C-style implementation.
Finally, we have three test functions that make sure the encoding and decoding worked correctly. These tests are based on the following premise: original_value = Decode(Encode(original_value)). If this premise holds for a large quantity of random inputs then the functions are likely correct.
std::string EncodeBase58Check(const std::vector<unsigned char>& vchIn)
{
// add 4-byte hash check to the end
std::vector<unsigned char> vch(vchIn);
uint256 hash = Hash(vch.begin(), vch.end());
vch.insert(vch.end(), (unsigned char*)&hash, (unsigned char*)&hash + 4);
return EncodeBase58(vch);
}
bool DecodeBase58Check(const char* psz, std::vector<unsigned char>& vchRet)
{
if (!DecodeBase58(psz, vchRet) ||
(vchRet.size() < 4)) {
vchRet.clear();
return false;
}
// re-calculate the checksum, ensure it matches the included 4-byte checksum
uint256 hash = Hash(vchRet.begin(), vchRet.end() - 4);
if (memcmp(&hash, &vchRet[vchRet.size() - 4], 4) != 0) {
vchRet.clear();
return false;
}
vchRet.resize(vchRet.size() - 4);
return true;
}
bool DecodeBase58Check(const std::string& str, std::vector<unsigned char>& vchRet)
{
return DecodeBase58Check(str.c_str(), vchRet);
}The last function is simply a utility that uses C++ meta-data to pass c_str() (C-style null terminated string) to the C implementation.
Well I hope you enjoyed this tour of one of Bitcon’s better known facets. The results of Base58 encoding along with some standard encoding practices are used by the entire Bitcoin community when they pass address hashes around.
Return to commented Bitcoin source code index.