256 Bit Integer commented uint256.cpp from Bitcoin Core source code

If you’ve developed systems in C or C++ before then you’re probably familiar with the stdint.h (cstdint for C++) typedefs. Since there’a lot of variation between platforms, stdint.h standardizes integer type names in an intuitive way. A uint8_t is an 8-bit unsigned integer and a uint64_t is a 64 bit unsigned integer.

What you won’t find on stdint.h, though, are 256 bit integer types!  Not in the foreseeable future at least.

So Bitcoin Core defines its own 256 bit data type so 256 bit hashes can be stored in a single object. Of course most end-user computers only handle up to 64 bits at a time in their CPU registers, so to work with 256 bits we need a bit of built-in algebra on the data type itself.

So let’s have a look at how the Bitcoin Core source works with these very large integers.

uint256.h

First thing we find on uint256.h is a declaration of a template base class for what the Bitcoin Core comment calls “fixed size blobs” :

template<unsigned int BITS>
class base_blob

If you’re not familiar with C++ then this bit of code may warrant some explanation. As you know C++ templates are resolved at compile time. We’re used to seeing typename‘s in template specifiers but this time we have a unsigned int value called BITS passed to it. What happens then when you have a literal value instead of a type?

In this case BITS is substituted for the specified integer value everywhere it shows up at compile time! This means that declaring a 256 bit blob or a 128 bit blob does no incurr in any runtime overhead – one specialized class is generated for each value.

Next we have the resource managed by base_blob:

static constexpr int WIDTH = BITS / 8;
    uint8_t data[WIDTH];

The constexpr specifier tells the compiler that WIDTH is more than just a constant. It’s a constant that can be determined at compile time because BITS is substituted for a plain number by the templating system.

In the case where BITS = 256, the expression BITS / 8 will become 32 at compile time so we’ll end up with static constexpr int WIDTH = 32;for a 256 bit class.

The next line uint8_t data[WIDTH]will be translated as uint8_t data[32]for 256 bits.

The default constructor simply zeroes out a WIDTH number of bytes (determined by sizeofoperator which knows this width because it was all resolved at compile time) in the data array:

base_blob()
    {
        memset(data, 0, sizeof(data));
    }

This guarantees that whatever blob is allocated, it’s all set to zero before it’s used.

Another constructor takes the blob in the form of a string:

explicit base_blob(const std::vector<unsigned char>& vch);

We’ll see how this works when we look at the implementation details.

A inline IsNull utility function is then defined:

bool IsNull() const
    {
        for (int i = 0; i < WIDTH; i++)
            if (data[i] != 0)
                return false;
        return true;
    }

IsNull simply rolls up the blob bytes looking for non-zero values. If any is found, it immediately short cuts and returns false. Otherwise if all bytes are zero, then it’s a null blob.

SetNull zeroes out the blob, copying zero to every byte in the blob:

void SetNull()
    {
        memset(data, 0, sizeof(data));
    }

Compare does a byte-wise comparison on two blobs using C function memcmp which subtracts each byte on the right operand from the left operand. If the left one is smaller it’ll yield a negative value, if it’s the same it’ll yield zero and if bigger it’ll yield a positive value.

The three next functions use Compare to derive the most common operators:

friend inline bool operator==(const base_blob& a, const base_blob& b) { return a.Compare(b) == 0; }
    friend inline bool operator!=(const base_blob& a, const base_blob& b) { return a.Compare(b) != 0; }
    friend inline bool operator<(const base_blob& a, const base_blob& b) { return a.Compare(b) < 0; }

Four string <-> blob functions are now declared. We’ll take a look at these at the implementation.

std::string GetHex() const;
    void SetHex(const char* psz);
    void SetHex(const std::string& str);
    std::string ToString() const;

Here we have C++ container-like functions that should look familiar to any CPP programmer:

unsigned char* begin()
    {
        return &data[0];
    }

    unsigned char* end()
    {
        return &data[WIDTH];
    }

    const unsigned char* begin() const
    {
        return &data[0];
    }

    const unsigned char* end() const
    {
        return &data[WIDTH];
    }

    unsigned int size() const
    {
        return sizeof(data);
    }

begin() returns a pointer to the first data item. end() returns a pointer to one byte past the end of data (This is important! end() points beyond the bounds of array memory!). The unsigned versions do the same, then we have size() which simply returns the same value as WIDTH which is the size of data in bytes.

Now we have an interesting function called GetUint64(int pos) which returns a slice of 64 bit unsigned integer from a 256 bit blob starting pos bytes from the beginning of data.

uint64_t GetUint64(int pos) const
    {
        const uint8_t* ptr = data + pos * 8;
        return ((uint64_t)ptr[0]) | 
               ((uint64_t)ptr[1]) << 8 | 
               ((uint64_t)ptr[2]) << 16 | 
               ((uint64_t)ptr[3]) << 24 | 
               ((uint64_t)ptr[4]) << 32 | 
               ((uint64_t)ptr[5]) << 40 | 
               ((uint64_t)ptr[6]) << 48 | 
               ((uint64_t)ptr[7]) << 56;
    }

First it sets ptr to pos bytes offset from the beginning of data. ptr now becomes our reference point from which 8 subsequent chunks of 64 bits each are all aligned and OR‘ed together.  If the first bit of the next 64 bit chunk is turned on, it’ll be turned on on the return value. If bit 3 of the 4th chunk is 1 then bit 3 of the returned value will be one as well.

It works a bit like the first stage of a bloom filter where bits are turned on for every chunk of a certain size ( here every 64 bit chunk after ptr ). The returned value is the result of OR’ing together all those chunks.

Next we have 2 utility I/O functions to read and write the blob onto a Stream:

template<typename Stream>
    void Serialize(Stream& s) const
    {
        s.write((char*)data, sizeof(data));
    }

    template<typename Stream>
    void Unserialize(Stream& s)
    {
        s.read((char*)data, sizeof(data));
    }

These two functions read and write the data to the stream in the same order it’s found on the buffer writing byte 0 first, then byte 1 and so on. Any numerical transformations from string to numbers and viceversa must be performed by the implementing class itself.

Then we have a specialization of our blob class as a 160 bit blob:

class uint160 : public base_blob<160>

160 bit blobs will be heavily used in the RIPEMD-160 code sections.

A specialization for 256 bit blobs:

class uint256 : public base_blob<256>

Finally two overloaded versions of inline uint256 uint256S where a std::string and a C style char* are converted to uint256.

/* uint256 from const char *.
 * This is a separate function because the constructor uint256(const char*) can result
 * in dangerously catching uint256(0).
 */
inline uint256 uint256S(const char *str)
{
    uint256 rv;
    rv.SetHex(str);
    return rv;
}
/* uint256 from std::string.
 * This is a separate function because the constructor uint256(const std::string &str) can result
 * in dangerously catching uint256(0) via std::string(const char*).
 */
inline uint256 uint256S(const std::string& str)
{
    uint256 rv;
    rv.SetHex(str);
    return rv;
}

uint256.cpp

uint256 is a curious case where the header file is actually more complex than the source code! We’ve covered a lot of ground in our header discussion, now let’s see what’s left in the Bitcoin Core implementation of 256 bit unsigned integers.

First we have a base_blob<BITS> constructor:

template <unsigned int BITS>
base_blob<BITS>::base_blob(const std::vector<unsigned char>& vch)
{
    assert(vch.size() == sizeof(data));
    memcpy(data, vch.data(), sizeof(data));
}

First it checks that the vector size is the same size of the allocated data array. Then it copies the vector data to the local data member variable.

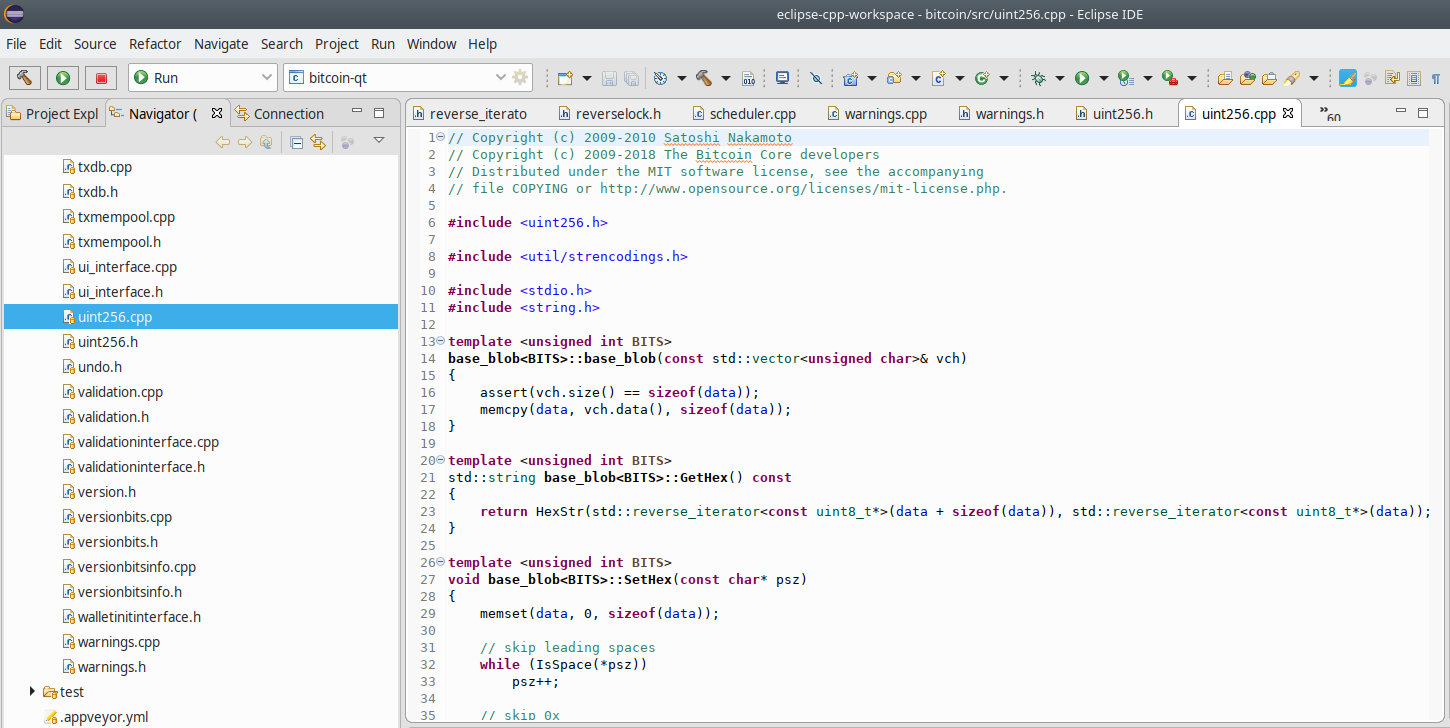
GetHex() returns the hexadecimal std::string representation of data:

template <unsigned int BITS>
std::string base_blob<BITS>::GetHex() const
{
    return HexStr(std::reverse_iterator<const uint8_t*>(data + sizeof(data)), std::reverse_iterator<const uint8_t*>(data));
}

GetHex() works by pointing the initial iterator to one item past the end of data and the end iterator to the beginning of data. HexStr() then iterates backwards, byte by byte while generating the return std::string.

SetHex(const char *psz)  takes a C-style string as input and interprets it as a hexadecimal number, setting data accordingly.

I’ll comment within the code snippet for practicity. As always, my comments beging with > while original source comments begin with // or /*

template <unsigned int BITS>
void base_blob<BITS>::SetHex(const char* psz)
{
> Set data to all anull bytes (zeroes)

    memset(data, 0, sizeof(data));

    // skip leading spaces
    while (IsSpace(*psz))
        psz++;

    // skip 0x
    if (psz[0] == '0' && ToLower(psz[1]) == 'x')
        psz += 2;

    // hex string to uint
    size_t digits = 0;

> HexDigit is a utility function imported from util/strencodings.cpp
> It looks hex digits up in table p_util_hexdigit. Returns -1 when
> invalid code is passed to it.
    while (::HexDigit(psz[digits]) != -1)
        digits++;

> p1 will now point to the beginning of data. Note it's a uchar data type (1 byte).
    unsigned char* p1 = (unsigned char*)data;

> pend will point one byte beyond the last character in data. 
> We discussed WIDTH at length earlier on.
    unsigned char* pend = p1 + WIDTH;

> Now we iterate backwards from last digit (higher mem addr) to first digit
> (lower mem addr). Remember : us humans write numbers in big endian form,
> Intel-based computers write them in little-endian!
> So while we still have digits and the end pointer is higher than the 
> beginning of data, repeat...
    while (digits > 0 && p1 < pend) {
> ...store psz[digits - 1] in p1
        *p1 = ::HexDigit(psz[--digits]);
>       if we still have digits...         
        if (digits > 0) {
>           ... multiply the digit by 16 (hexadecimal base)
>               and then OR it (binary addition) with the value in p1
            *p1 |= ((unsigned char)::HexDigit(psz[--digits]) << 4);
>           increment the p1 pointer to set the next digit
            p1++;
        }
    }
}

Now we have a version of SetHex for C++ std::strings which simply calls the c_str() method to return a pointer to a C-style string. Then it calls the C string version we just discussed:

template <unsigned int BITS>
void base_blob<BITS>::SetHex(const std::string& str)
{
    SetHex(str.c_str());
}

A ToString() method is provided. It just calls GetHex().

template <unsigned int BITS>
std::string base_blob<BITS>::ToString() const
{
    return (GetHex());
}

Finally we have a bit of a C++ hack that forces the compiler to add the 160 and 256 bit templated codes into libraries explicitly. Let’s take a look at the code and then I’ll comment.

// Explicit instantiations for base_blob<160>
template base_blob<160>::base_blob(const std::vector<unsigned char>&);
template std::string base_blob<160>::GetHex() const;
template std::string base_blob<160>::ToString() const;
template void base_blob<160>::SetHex(const char*);
template void base_blob<160>::SetHex(const std::string&);

// Explicit instantiations for base_blob<256>
template base_blob<256>::base_blob(const std::vector<unsigned char>&);
template std::string base_blob<256>::GetHex() const;
template std::string base_blob<256>::ToString() const;
template void base_blob<256>::SetHex(const char*);
template void base_blob<256>::SetHex(const std::string&);

As you can see no variable is being declared nor is anything getting defined.

What’s happening here is we’re telling the compile-time templating engine to generate this code which does nothing at the end of the source file. This forces the compiler to insert the 160 and 256 bit specializations of base_blob into the binary library code!

Since the idea is to extract libraries from the Bitcoin Core source, so that other software can link to it dynamically, if we compiled this code without linkage to an actual use of the 160 and 256 bit blobs, the code would be simply dropped as unused templates do not necessarily get included in object files when they’re not used.

UINT256 in Other Languages

The Ethereum Virtual Machine (EVM) has native 256 bit word size. Thus, uint256 is a basic type (not a composite object) on all Solidity smart contracts.

Here’s a TypeScript uint256 implementation.

There’s an Ethereum API implementation for Haskell, where uint256’s are available.

In Rust you’ll find a type called num256, which is roughtly equivalent to uint256 in C and C++.

Python will automagically convert your integers to bignum’s if you happen to need it. Thus, python has become a popular programming language for cryptocurrency payment systems. You don’t need to do anything for a Python integer to become a uint256 or larger – if a number overflows, Python will automatically switch to bignum mode. (Speed being the tradeoff, of course.)

Here’s an example C# implementation which allows you to compare string hashes.

Javascript makes things a bit more complicated when it comes to large numbers. In fact, JS sometimes balks at numbers with more than 15 digits. For large number calculation in JS, you’ll need a bignum library. The Ethereum web3.js library also probably covers uint256 in Javascript.

How long will the UNIT256 space last?

Here’s a nice back of the envelope calculation about how long an uint256 would last under certain situations.

Say everyone around the world (the above example uses only USA, but it doesn’t matter in this case) kept increasing a number every second for an entire year. You’d use up around 10 to the 16th power worth of numbers. Since uint256 is around 10 to the 77th power, you’d have a 61 zeroes-size number of units left to use. This amount of time is more than the universe will ever last.

Return to Bitcoin Source Code commentary index

uint256 Converter

Python is the best uint256 converter available, because it natively converts any number larger than its largest internal integer into a bignum, which can process arbitrarily large numbers.

For example, Python easily converts the maximum uint256 value to HEX:

>>> hex(2**256)
'0x10000000000000000000000000000000000000000000000000000000000000000'

Well that’s not such a good example, since 2^256 is a round hexadecimal power. Anyway, any uint256 can be handled natively in Python. All integer functions work just fine, so if you need to convert it to some other base or multiply, add, subtract or do large number cryptography, such as RSA, it’s really easy in Python.

Here’s another Python example, say you need to convert some large uint256 to a decimal format: Convert UINT256 to a readable number

uint256 Maximum Value

The maximum value of a 256 bit number is 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,936 

It’s easy to check that this value is correct using the Python REPL:

$ python3
Python 3.8.5 (default, Jul 28 2020, 12:59:40) 
[GCC 9.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> 2**256
115792089237316195423570985008687907853269984665640564039457584007913129639936

Technically, the largest value a 256 bit integer can take is the above number minus 1.

It’s OK to overflow by 1 in Python, but it’d likely spell trouble in C or C++.

Links

uint256.h Bitcoin Source at Github

Bitcoin cryptography library

Understanding blockchain by code – 1

What is the maximum input value for function uint256 parameter?

Compile, Run, And Customize Your Own Bitcoin Client

How to make an altcoin

Bitcoin.org : Bitcoin development

How to convert uint256 to bytes, and bytes convert to uint256